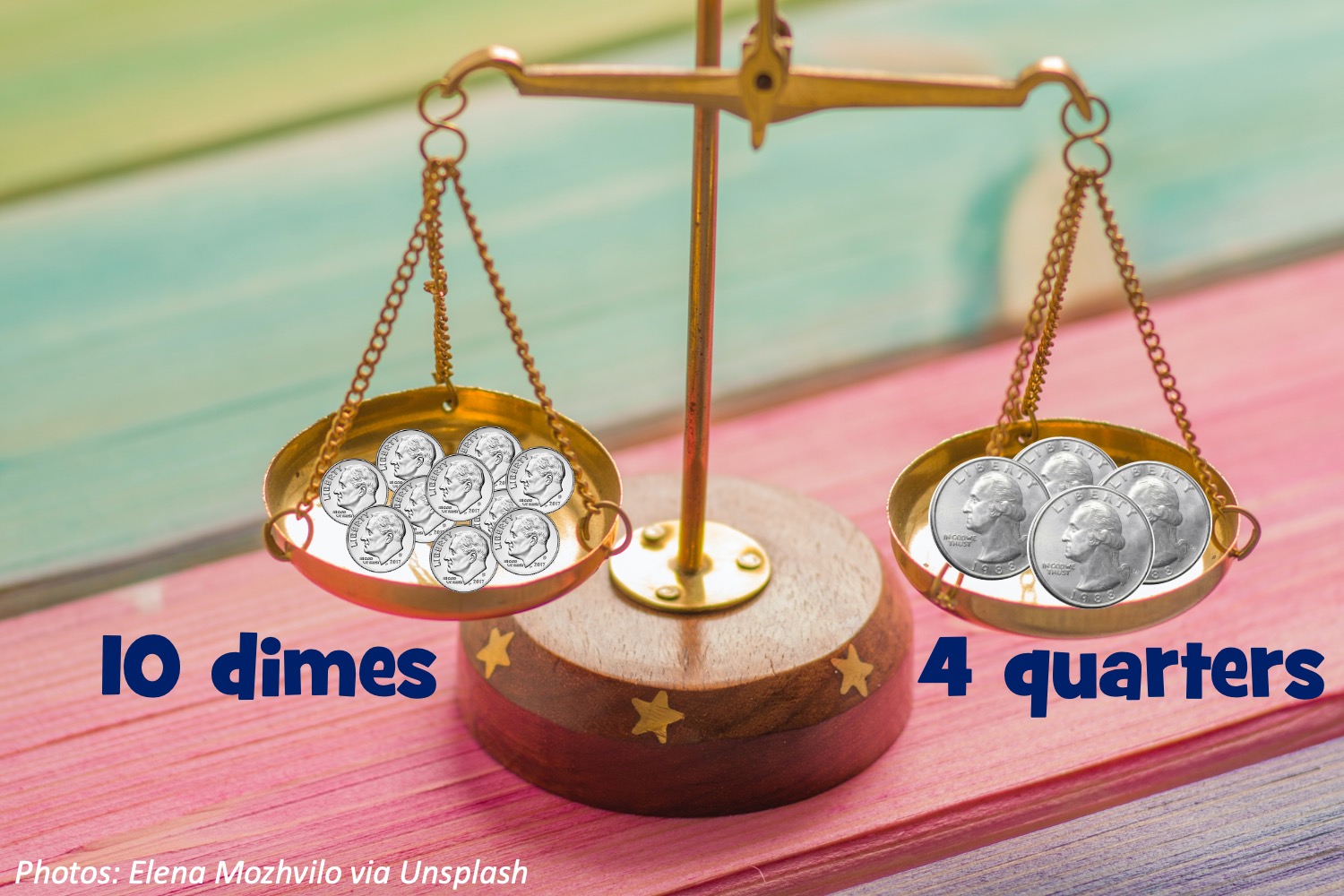When we count out money to pay for something, usually we don’t study it very carefully – we just add it up. But money has some cool secrets. Here in America, the same value of dimes and quarters will also weigh the same: a dollar’s worth of dimes will perfectly balance a dollar of quarters. Also, 5 quarters weighs exactly an ounce, so each weighs 1/5 of an ounce. Then there are those ridges around the edge: a dime has 118 ridges (called “reeds”) while a quarter has 119 of them (was one of those an accident?). We aren’t sure why coins have ridges: one theory is that back when coins were made of real gold and silver, people would shave bits of metal off the edges and sell the shavings, so ridges kept people from getting away with that. Nickels and pennies never needed the ridges since those use cheaper metals. But either way, every coin in your pocket counts for something.
Wee ones: A U.S. dime is worth 10 cents, and a quarter is worth 25 cents. Which coin is worth more?
Little kids: A dime is 10 cents, and a dollar is 100 cents. How many dimes do you need to make a dollar? Bonus: If you also have a dollar of quarters, how many coins do you have in total? (Hint if needed: Why is a quarter called a “quarter”?)
Big kids: If you have 10 quarters and your friend has 30 dimes, whose pile of coins weighs more? Bonus: If you want $9.40 of vending-machine treats and need the most dimes and quarters possible in equal weights, how many nickels will you need to fill in the rest?
Answers:
Wee ones: The quarter.
Little kids: 10 dimes. Bonus: 14 coins: 10 dimes and 4 quarters.
Big kids: Your friend’s, since he has $3.00 and that equals the weight of 12 quarters, of which you have only 10. Bonus: 8 nickels. If you could do all dimes and quarters, you’d need $4.70 of each, which isn’t divisible by 25 cents. So you’ll need $4.50 of quarters and $4.50 of dimes, leaving you 40 cents short.
